Применение ООП на практике

• Dive in в доменную область
• Постановка задачи
  • Предпосылка
  • Задача
  • Ожидаемый результат
• Алгоритм решения
• Процедурное решение
• Объектно-ориентированное решение
  • А зачем?
  • Теория
  • Код
• Выводы

Чаще всего задачу можно решить интуитивно понятным процедурным способом. Однако самый простой вариант не всегда самый лучший. Предлагаю посмотреть на примере реальной задачи, как можно сделать решение объектно-ориентированным, и какую пользу это может принести.

Dive in в доменную область

В PVS-Studio мы разрабатываем статический анализатор кода, а наша ежедневная работа — создание новых диагностических правил, которые могут обнаружить потенциальные ошибки в коде. Про принципы работы статического анализа можно почитать тут, а конкретно про Java анализатор — здесь. Однако для понимания задачи нам хватит объяснения общих принципов работы лишь двух из наших инструментов: синтаксического дерева и семантической модели.

Итак, у нас есть синтаксическое дерево, состоящие из элементов кода программы. Не стану умничать и приведу схему из указанной выше статьи:

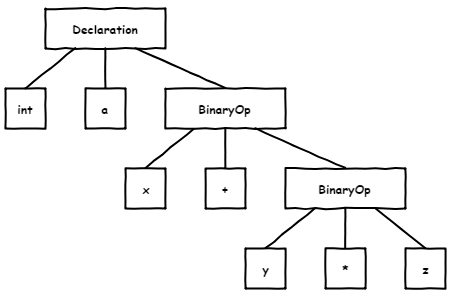
Как можно догадаться, это — дерево разбора для следующего кода:

int a = x + y * z;

Кроме этого, в нашем распоряжении различная семантическая информация про каждый из узлов: тип, место объявления переменных и пр. С базой закончили! Остальное разберём по ходу дела. Для простоты понимания информации кое-где я срежу углы и намеренно упрощу API.

Постановка задачи

Предпосылка

Требуется разработать следующее диагностическое правило: обнаружение переменной действительного типа в качестве счётчика цикла for. Его реализация тривиальная: надо просто проверить тип переменных-счётчиков (плюс обработать особые случаи, вроде циклов вида for (;;)). Далее встаёт вопрос об уровне предупреждения. И вот тут начинается самое интересное.

Одним из основных рисков использования счётчиков действительного типа являются лишние — либо недостающие — итерации. Учитывая, что for часто определяют как цикл с заранее известным количеством итераций, в его случае такое поведение является наиболее губительным. Но ведь на практике далеко не всегда люди пользуются инструментами по их прямому назначению (цикл for можно использовать аналогично while). И как нам отличить одно намерение программиста от другого? Эвристика!

Задача

Имеем следующее правило: если значения всех переменных в объявлении цикла можно получить из контекста метода, то программист явно ожидал определённого числа итераций. В таком случае мы выдаём предупреждение второго уровня. Иначе мы не можем быть уверены в намерениях программиста и выдаём третий уровень.

Ожидаемый результат

Эталонный случай — все значения прямо в объявлении цикла — для предупреждения второго уровня:

for (double i = 0.0; i < 1.0; i += 0.1) { }

Но нам надо найти и такие случаи:

double lowerBoundary = 0.5;
for (double i = lowerBoundary; i < 1.0; i += 0.1) { }

И такие:

double shift = 0.5;
double lowerBoundary = 0.0 + shift;
double upperBoundary = 1.0;
for (double i = lowerBoundary; i < shift + upperBoundary; i += 0.1) { }

В случае же, если значения в цикл попали извне — поля объектов или параметры методов, — мы выдаём третий уровень.

Алгоритм решения

Итак, у нас есть узел синтаксического дерева с объявлением цикла for, а вернуть нам надо true или false в зависимости от того, все ли значения можно получить из локального контекста.

В каждой из секций цикла: инициализации счётчиков, их изменение и условие остановки — надо будет проверить источник значений в выражениях.

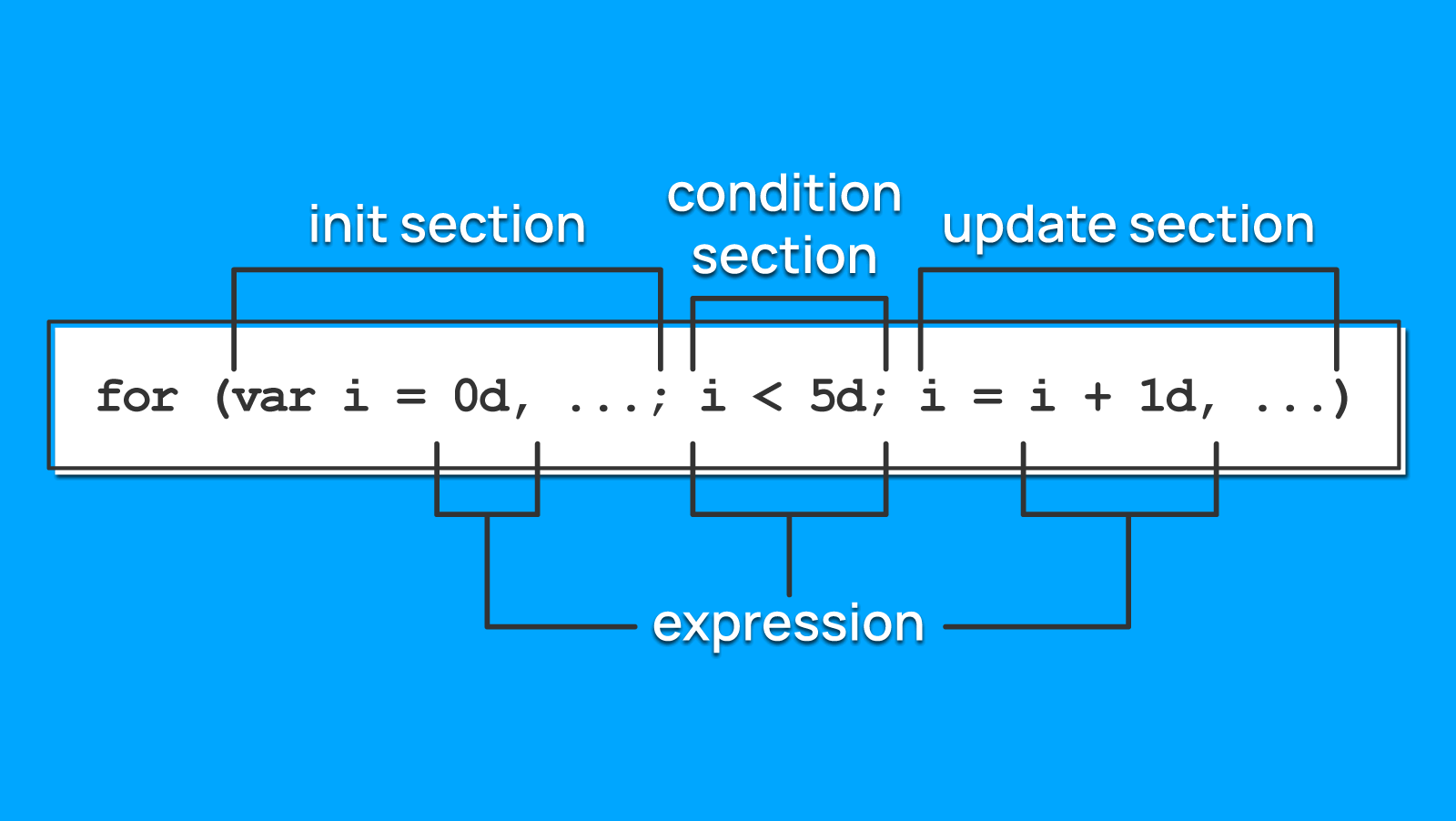
Выражения могут состоять из следующих элементов:

• Литералы, наличие которых нас и интересует;
• Унарные и бинарные операторы: их надо просто раскрыть;
• Переменные: нужно обработать выражение, полученное из их инициализации;
• Любые другие: поле класса, параметр и пр. В этом случае обход можно останавливать.

Очевидно, недостаточно просто посмотреть соседние узлы в синтаксическом дереве, ведь выражения могут состоять из других подвыражений, а одни переменные зависеть от других. Поэтому нам нужен способ обойти всё дерево целиком, не ограничиваясь только соседними узлами (и теми, что получены из семантического анализа).

Условием остановки будет обход всех терминальных узлов (таких, что не имеют дочерних узлов). Если все терминальные узлы в обходе — это литералы, то значение является предсказуемым. В обратном случае фиксируется непредсказуемость.

Процедурное решение

Итак, нам нужно обойти дерево неизвестной глубины. Классическое решение — рекурсия. Напишем метод isAccessible, который принимает на вход некоторое выражение, после чего раскрывает его и определяет доступность источника значений.

private static boolean isAccessible(CtCodeElement el) {
  return isAccessible(el, Collections.emptyList());
}

private static boolean isAccessible(
  CtCodeElement el,
  List<CtVariable> exclude
) {
  if (isCodeElementEqualsToAny(el, exclude)) {
    return true;
  }

  var expressionElements = new LinkedList<CtCodeElement>();
  parseExpression(el, expressionElements);
  return expressionElements.stream().allMatch(x -> x instanceof CtLiteral);
}

private static void parseExpression(
  CtCodeElement el,
  List<CtCodeElement> terminalNodes
) {
  if (el instanceof CtBinaryOperator) {
    var op = (CtBinaryOperator) el;
    parseExpression(op.getLeftHandOperand(), terminalNodes);
    parseExpression(op.getRightHandOperand(), terminalNodes);
  } else if (el instanceof CtUnaryOperator) {
    parseExpression(((CtUnaryOperator)el).getOperand(), terminalNodes);
  } else if (el instanceof CtVariable) {
    parseExpression(Optional.ofNullable(((CtVariable)el).getDeclaration())
                            .map(CtDeclaration::getDefaultExpression)
                            .orElse(null), terminalNodes);
  } else {
    terminalNodes.add(el);
  }
}

Самая сложная работа сделана. Осталось получить выражения из каждой секции цикла. В секции инициализации всё просто: счётчик может объявляться либо прямо в этой секции, либо используется уже существующая переменная. В любом случае нас интересует лишь выражение, результат которого присваивается счётчику. Счётчиков может быть более одного, так что это мы тоже учитываем.

public boolean areInitsPredictable() {
  return init.stream().allMatch(x -> {
    if (x instanceof CtLocalVariable) {
      return isAccessible(((CtLocalVariable)x).getDefaultExpression());
    } else if (x instanceof CtAssignment) {
      return isAccessible(((CtAssignment)x).getAssignment());
    } else {
      return false;
    }
  });
}

С условием проще всего: лишь проверяем, что это вообще бинарный оператор (иначе у нас лапки), после чего раскрываем и проверяем операнды.

public boolean isConditionPredictable(
  List<CtVariableReference> initReferences
) {
  var operator = safeCast(condition, CtBinaryOperator.class);
  if (operator == null)
    return false;

  return Stream.of(
    operator.getLeftHandOperand(),
    operator.getRightHandOperand()
  ).allMatch(x -> isAccessible(x, initReferences));
}

И напоследок секция изменения счётчиков. Здесь всё почти аналогично: бинарный оператор раскрываем, а на унарных — например, инкрементах — сразу останавливаемся.

public boolean areUpdatesPredictable(
  List<CtVariableReference> initReferences
) {
  return update.stream().allMatch(x -> {
    if (x instanceof CtAssignment) {
      return isAccessible(
        ((CtAssignment)x).getAssignment(),
        initReferences
      );
    } else {
      return x instanceof CtUnaryOperator;
    }
  });
}

И соединяем всё это воедино:

public boolean areAllValuesPredictable() {
  var initReferences = getInitReferences();
  return    areInitsPredictable()
         && isConditionPredictable(initReferences)
         && areUpdatesPredictable(initReferences);
}

Всё готово! Код работает, тесты проходят, потенциальные ошибки находятся.

Объектно-ориентированное решение

А зачем?

Процедурный код вполне читаемый, решение выполняет задачу. Разве тут можно что-то улучшить?

Вопрос, конечно, дискуссионный, ибо KISS, YAGNI и всё такое. Но всё же стоит иногда вспоминать, что работа не ограничивается рамками одной задачи, из-за чего имеет смысл мыслить шире. Синтаксический и семантический анализы — не все инструменты анализатора, но одни из самых базовых. И, разумеется, используем мы их часто.

Так вот, если принять гипотезу, что обход синтаксического дерева в нашем случае будет требоваться очень часто, то такой код следует переиспользовать. Но очевидно, что "как есть" применять тот же метод parseExpressions получится не всегда. Может, мы захотим изменить поиск в глубину на поиск в ширину, или выбрать ещё более изящный алгоритм обхода дерева. А может, нам понадобятся другие правила разворачивания выражений или получения семантической информации (например, раскрывать элементы массива).

Конечно, можно перенести методы в утилитный класс и провести рефакторинг, но после некоторого количества итераций код предсказуемо превратится в спагетти. Чувствуете? Это же предпосылка для использования паттернов!

Теория

ООП

Решили: делаем решение на основе ООП. Но как именно нам достигнуть результата? Инкапсулировать необходимое поведение нам помогут классические паттерны проектирования. Не стану забирать себе лавры GoF и тысяч других людей, которые уже их описывали, но быстро напомнить считаю необходимым.

Итератор

Учитывая, что почти вся задача строится на обходе синтаксического дерева, итератор напрашивается сам собой. Классическая диаграмма классов для него выглядит так.

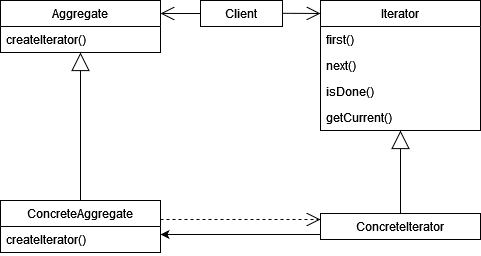
С самим итератором всё понятно: мы можем перемещаться, получать текущий элемент и определять, когда обход закончен.

Под агрегатом чаще всего понимается коллекция, по которой будет происходить итерация. Но постойте! Внимательный читатель должен был подметить, что на вход нам давался некоторый элемент дерева, но не какая-то коллекция сама по себе.

И тут время абстрагироваться. Ведь мы обходим не только само дерево (раскрытие операторов), но ещё и ищем инициализацию переменных (переходим в совсем другие узлы этого дерева). То есть эта "коллекция" очень абстрактна и существует только у нас в голове. Не совсем по паттерну получается... К счастью, паттерны не являются сводом строгих правил, так что мы со спокойной душой сможем от них отойти и забыть про всю левую часть диаграммы.

Стратегия

Хорошо, мы договорились, что итератор должен инкапсулировать в себе поведение обхода некоторого — абстрактного — множества элементов. Но мы, кажется, хотели, чтобы при необходимости можно было реализовывать разные стратегии обхода? Ну вот, само вырвалось :).

Мы, конечно, могли бы реализовывать их в разных конкретных итераторах, но вот незадача: типов этих стратегий может быть много. Как я и говорил, мы можем захотеть поменять алгоритм обхода коллекции с ширины на глубину, а можем поменять сам принцип раскрытия узлов (в нашем случае — добавлять узлы из семантической информации). И если бы мы соединили эти алгоритмы в одном конкретном итераторе, то получили бы комбинаторное увеличение типов итераторов.

Работа с композицией вместо наследования решает эту проблему, так что тип алгоритма обхода я предлагаю оставить в итераторе, а раскрытие узлов инкапсулировать в стратегию. Её стандартная диаграмма выглядит так.

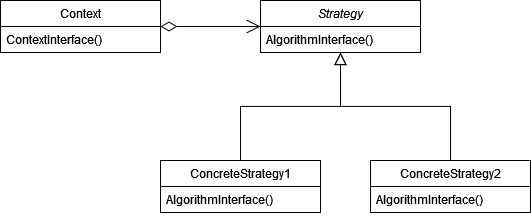
В нашем случае контекстом будет сам итератор, в остальном всё должно быть ясно. Осталось только решить вопрос, как мы распределим поведение обхода между разными стратегиями.

Шаблонный метод

Ещё одна гипотеза: раскрытие операторов является настолько частой операцией, что мы считаем такое поведение поведением по умолчанию. В таком случае альтернативный метод раскрытия узла можно вынести в зацепку, которая является частным случаем шаблонного метода. Его схема показана ниже.

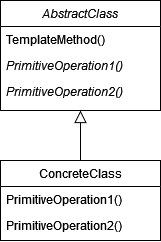
На этом повторение необходимой теории можно закончить и наконец-то перейти к практике.

Код

Переходим к реализации. И начнём мы, как и в прошлый раз, с раскрытия узлов. В данном случае — с реализации стратегии.

В её качестве введём класс TreeNode, который инкапсулирует в себе поведение раскрытия таких узлов и имеет зацепку для реализации альтернативных стратегий. Непосредственно разворачивание выражения происходит в методе getChildrenInternal, который имеет возможность использовать переопределённый в потомках getChildrenHook.

public class TreeNode {
  private CtCodeElement element; 
  private List<CtCodeElement> children = null;

  public TreeNode(CtCodeElement element) {
    this.element = element;
  }

  public final CtCodeElement getElement() {
    return element;
  }
  public final void setElement(CtCodeElement element) {
    this.element = element;
    children = null;
  }

  // Метод, реализующий поведение раскрытия узлов
  private List<CtCodeElement> getChildrenInternal() {
    var current = getElement();
    if (current instanceof CtLiteral) {
      return Collections.emptyList();
    }
    var children = getChildrenHook();
    if (children != null) {
      return children;
    } else if (current instanceof CtBinaryOperator) {
      CtBinaryOperator op = (CtBinaryOperator) current;
      return Arrays.asList(op.getLeftHandOperand(),
                           op.getRightHandOperand());
    } else if (current instanceof CtUnaryOperator) {
      return Collections.singletonList(
        ((CtUnaryOperator) current).getOperand()
      );
    } else {
      return Collections.emptyList();
    }
  }
  protected List<CtCodeElement> getChildrenHook() {
    return null;
  }

  // Обёрточные методы для использования кэша узлов
  public List<CtCodeElement> getChildren() {
    if (children == null) {
      children = getChildrenInternal();
    }
    return children;
  }
  public boolean hasChildren() {
    if (children == null) {
      children = getChildrenInternal();
    }
    return !children.isEmpty();
  }
}

Место инициализации переменной этот алгоритм не найдёт. Это мы оставим потомкам. Вернёмся в класс диагностики и добавим туда метод, возвращающий анонимный класс.

private TreeNode createDeclarationFinderNode(CtCodeElement el) {
  return new TreeNode(el) {
    @Override
    public List<CtCodeElement> getChildrenHook() {
      var el = this.getElement();
      CtExpression expr = null;

      if (el instanceof CtLocalVariable) {
        expr = ((CtLocalVariable) el).getDefaultExpression();
      } else if (el instanceof CtAssignment) {
        expr = ((CtAssignment) el).getAssignment();
      } else if (el instanceof CtVariable) {
        expr = Optional.of(((CtVariable) el))
                       .map(CtVariable::getDeclaration)
                       .map(CtDeclaration::getDefaultExpression)
                       .orElse(null);
      }

      return expr != null ? Collections.singletonList(expr)
                          : null;
    }
  };
}

Теперь, если мы встретим на пути переменную, то к синтаксическому анализу добавится семантический, и мы сможем добавить новые узлы для обхода.

Остался лишь сам итератор. Помимо отсутствия агрегата позволю себе ещё вольностей и сделаю интерфейс немного меньше того, что был указан на диаграмме. first() нам не нужен, а вместо isDone() буду использовать getCurrent(), возвращающий null. Поведение раскрытия узлов определяется типом TreeNode, переданным в конструктор, поэтому из логики здесь остался алгоритм обхода по умолчанию — в ширину.

public class TreeIterator {
  private final TreeNode currentNode;
  private final LinkedList<CtCodeElement> unfoldedNodes = new LinkedList<>();

  public TreeIterator(CtCodeElement node) {
     currentNode = new TreeNode(node);
  }
  // Конструктор для создания итератора с потомком TreeNode
  public TreeIterator(
    CtCodeElement node,
    Function<CtCodeElement, TreeNode> constructor
  ) {
    currentNode = constructor.apply(node);
  }

  public CtCodeElement getCurrentNode() {
    return currentNode.getElement();
  }
  public boolean isTerminalNode() {
    return !currentNode.hasChildren();
  }

  public CtCodeElement next() {
    var children = currentNode.getChildren();
    if (children != null)
    unfoldedNodes.addAll(children);

    if (unfoldedNodes.isEmpty())
      return null;

    currentNode.setElement(unfoldedNodes.pop());
    return currentNode.getElement();
  }
}

Ну и наконец адаптируем уже написанные в процедурной части методы (не встречавшиеся ранее вызовы методов объяснены в той же части).

Для начала сделаем аналоги isAccessible, но чётко направленные на выявление соблюдения условия: в терминальном узле не должно быть ничего, кроме литерала (исключение для сравнения — сам счётчик).

private static boolean isPassable(TreeIterator iterator, CtCodeElement el) {
  return !iterator.isTerminalNode() || el instanceof CtLiteral;
}

private static boolean isPassableOrExcludes(
  TreeIterator iterator,
  CtCodeElement el,
  List<CtVariableReference> exclude
) {
  return isPassable(iterator, el) 
      || el instanceof CtVariable && isCodeElementEqualsToAny(el, exclude);
}

А теперь можно со спокойной душой переделать инициализацию.

private boolean areInitsPredictable() {
  for (var el : init) {
    var iterator = new TreeIterator(el, this::createDeclarationFinderNode);
    for (var node = iterator.getCurrentNode();
         node != null;
         node = iterator.next()
    ) {
      if (!isPassable(iterator, node)) {
        return false;
      }
    }
  }
  return true;
}

Таким же образом обработать условие.

private boolean isConditionPredictable(
  List<CtVariableReference> initReferences
) {
  var iterator = new TreeIterator(condition, this::createDeclarationFinderNode);
  for (
    var node = iterator.getCurrentNode();
    node != null;
    node = iterator.next()
  ) {
    if (!isPassableOrExcludes(iterator, node, initReferences)) {
      return false;
    }
  }
  return true;
}

И изменение счётчиков. Дополнительная логика аналогична таковой в процедурной части.

private boolean areUpdatesPredictable(
  List<CtVariableReference> initReferences
) {
  return update.stream()
               .allMatch(
    x -> {
      if (x instanceof CtAssignment) {
        var iterator = new TreeIterator(x, this::createDeclarationFinderNode);
        for (
          var node = iterator.getCurrentNode();
          node != null;
          node = iterator.next()
        ) {
          if (!isPassableOrExcludes(iterator, node, initReferences)
          ) {
            return false;
          }
        }
        return true;
      }
      else {
        return x instanceof CtUnaryOperator;
      }
  });
}

Общий метод без изменений.

public boolean areAllValuesPredictable() {
  var initReferences = getInitReferences();
  return    areInitsPredictable()
         && isConditionPredictable(initReferences)
         && areUpdatesPredictable(initReferences);
}

Вот и всё! Функционально код аналогичен написанному ранее, но теперь написан в объектно-ориентированном стиле, из-за чего его можно переиспользовать и расширять. Но и разобраться тоже стало немного сложнее, спорить не стану :).

Выводы

Надеюсь, у меня получилось продемонстрировать, как рядовую задачу с очевидным процедурным решением можно переставить на рельсы объектно-ориентированного программирования. Конечно, можно поставить под сомнение введённые в тексте гипотезы и обвинить меня в оверинжиниринге, но тема выбора подходов как таковая всё же за рамками этой заметки.

В комментариях можете поделиться, стоит ли продолжать рассказывать о применении паттернов на практике? Хорошо ли раскрыта тема на фоне статического анализа?

Кстати, диагностика из этой статьи войдёт в PVS-Studio 7.29. Если хотите попробовать её в деле, то можете перейти по этой ссылке.

А чтобы следить за выходом новых статей про качество кода, можете подписаться на:

• Твиттер PVS-Studio;
• Наш ежемесячный дайджест статей;
• Мой личный блог.